Skip to main content

FGV MBA Gestão Empresarial

11 Matemática financeira

11.1 Conceitos fundamentais

  • VDT: Valor do dinheiro no tempo

Um mesmo valor unitário vale mais recebendo hoje que no futuro

  • Aplicações da matemática financeira: Comparar a melhor relação de uso do dinheiro no tempo

Representação gráfica de um fluxo de caixa:

Onde:

  1. Seta para cima quer dizer dinheiro que você recebe
  2. Seta para baixo quer dizer dinheiro que você paga (ou investe)
  • Relação fundamental da matemática financeira:
  1. VP (Capital [C]): Chamado de valor presente, representa o valor monetário de aplicação ou recebimento no tempo presente
  2. VF (Montante [J]): Chamado de valor futuro, representa o valor monetário de pagamento ou recebimento no tempo futuro
  3. i (Taxa de juros): Percentual de aplicação sobre o capital no tempo. Podendo ser de regime simples ou composto
  4. J (Juros): Valor monetário da aplicação da taxa de juros no tempo.
  5. n (Período de tempo): Período em que o pagamento/investimento é atribuído.
  6. PMT (Pagamentos): Quantidade de pagamentos fixos ou variáveis que são atribuídos em cada período de tempo durante o ciclo de tempo
  • Definição dos regimes:
  1. Regime de juros simples: Os juros são sempre calculados sobre o saldo inicial

Variações da fórmula juros simples 1:

  1. Regime de juros compostos: Os juros são sempre calculados sobre o saldo atual

Variações da fórmula juros compostos:

Gráfico comparativo juros simples versus juros compostos:

  • Períodos de cálculo

11.2 Taxas de juros

Tipos de taxas:

  1. Taxa nominal: Trata-se de uma taxa de referência, É dada em UMA unidade de TEMPO, e a capitalização é dada em OUTRA unidade de TEMPO. Precisa ser CONVERTIDA para a unidade de tempo do prazo da capitalização

Ex: A taxa de 48% ao ano para pagamentos mensais

  1. Taxa Efetiva: Taxa que pode ser utilizada para as contas financeiras

A taxa de 48% ao ano para pagamentos mensais é de 4% ao mês

As equivalências das taxas são feitas da seguinte maneira:

  1. Equivalências de taxa de juros simples:

Basta multiplicar/dividir pela razão de transferência dos períodos.

  1. Equivalência de taxa de juros composta:

Basta elevar pelo número de períodos, caso seja de período longo para curto, eleva-se usando 1/n

  1. Taxa real: Taxa efetiva considerando a inflação

onde:

  • taxa i: taxa efetiva

Exemplo:

Observe que o montante não faz diferença na análise

  1. Taxa Over: Também chamada de overnight, trata-se do uso da taxa efeitiva considerando apenas os dias úteis

Onde:

ie = Taxa efetiva over = Taxa overnight du = Dias úteis

Exemplo:

11.2.1 Títulos prefixados e pós-fixados

As operações de mercado podem ser classificadas em:

  • operações de renda fixa (títulos ou fundos, por exemplo)
  • operações de renda variável (ações, por exemplo).

Uma operação de renda fixa pode ser:

  1. Renda prefixada: O aplicador e o devedor conhecem, no dia da transação, a taxa de retorno e também o valor do título no dia do resgate (encerramento).

  2. Renda pós-fixada: O aplicador e o devedor só conhecerão no dia da liquidação (encerramento) da transação a taxa de retorno e também o valor do título. Geralmente, uma parte fixa mais uma parte variável, que é definida a algum índice.

Exemplo de avaliação de investimentos das rendas:

11.3 Operações de desconto

Uma das operações mais frequentes no dia a dia dos mercados são as operações de desconto. Operações dedesconto visam à antecipação de um montante, valor a receber em uma data no futuro, para podermos dispordesse capital hoje.

Tipos de operação de desconto:

  • Desconto simples:

No regime de capitalização simples, temos três tipos de descontos:

  1. Desconto racional simples: Trata-se do cálculo do VP da taxa de juros simples
  2. Desconto comercial simples: No desconto por fora, os juros são calculados sobre o valor futuro
  3. Desconto bancário: No mundo real, além das taxas de juros, os bancos comerciais costumam cobrar uma taxa de administraçãopara realizar operações com desconto
  • Desconto composto:

No regime de capitalização composta, temos dois tipos de descontos:

  1. Desconto racional composto: Trata-se do cálculo do VP da taxa de juros composta
  2. Desconto comercial composto: Desconto sobre o valor nominal (montante) do título.

Desconto com vários títulos:

Na prática, não se opera com um título isoladamente. Em geral, desconta-se um conjunto de títulos com prazos de vencimento distintos.

Ex:

11.4 Séries de pagamentos

11.4.1 Séries uniformes

São fluxos de caixa iguais que se repetem em períodos regulares, podendo ser do tipo:

  1. Finitas: Possuem um período de pagamentos (ou recebimentos) constantes
  2. Infinitas (Perpetuidade): Perpetuidade é um conjunto de pagamentos (ou recebimentos) que não acabam mais, duram para sempre, são eternos.

As formas de manipulação do fluxo de caixa podem ser dos tipos:

  1. Postecipadas (VF): Trata-se em definir o valor futuro do fluxo de caixa
  2. Antecipadas (VP): Trata-se em definir o valor presente do fluxo de caixa
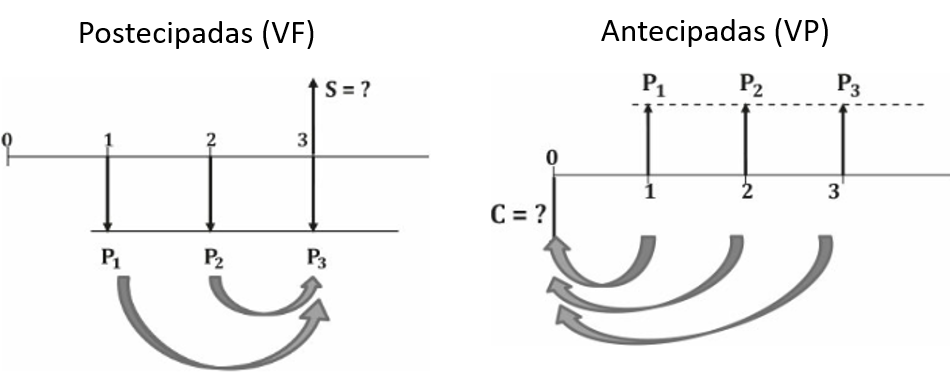
  1. Fórmulas fluxo de caixa finitas:

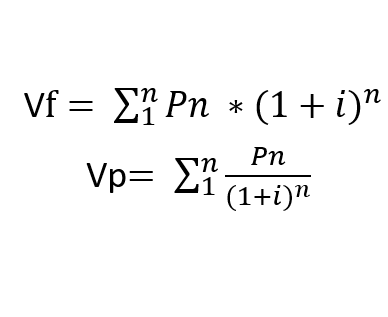
Onde:

Pn = Pagamentos de cada período

  1. Fórmulas fluxo de caixa perpetuidade:

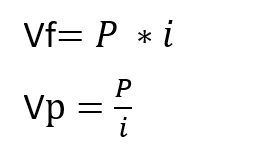
11.4.2 Séries de pagamentos não uniformes

O conceito é o mesmo, mas atribui-se a pagamentos de diferentes valores.

Para isto é utilizado em softwares o conceito de valor presente líquido (VPL/NPV) e taxa interna de retorno (TIR/IRR)

11.4.2.1 Valor presente Líquido (VPL)

Trata-se do cálculo do valor presente dado diferentes valores de pagamentos.

FinancialMath::NPV(cf0 = 1000, cf = c(100,200,100,400, -500,200,600,150), times = c(1,3,3,4,3,5,6,2), i =  0.02, plot = T)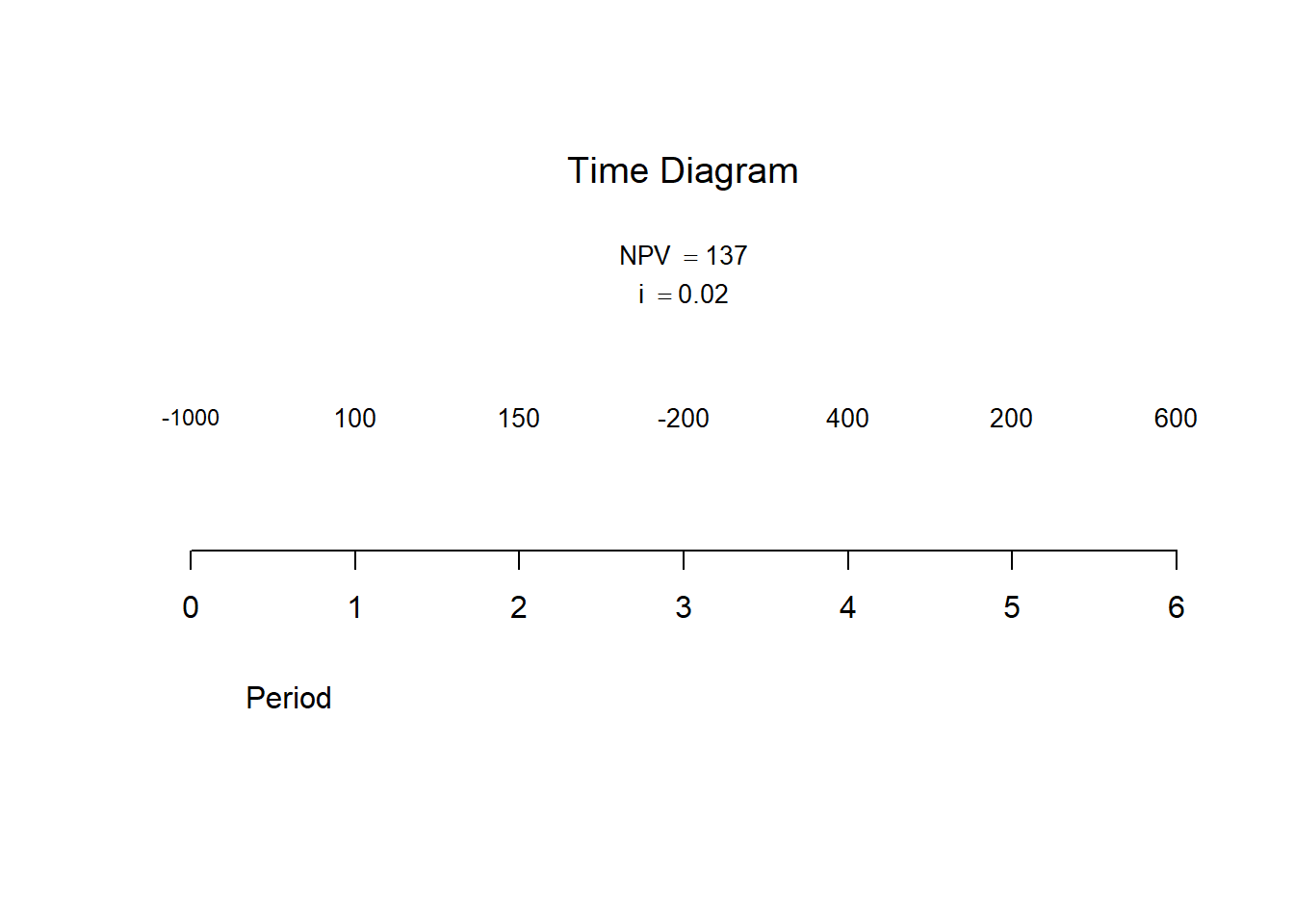
#> [1] 137

O VPL é muito utilizado em análise de investimentos, onde se identifica se os resultados de um investimento inicial são capazes de gerar retorno.

VLP > 0 -> Retorno positivo VPL < 0 -> Retorno negativo

11.4.2.2 Taxa interna de retorno (TIR)

Trata-se da taxa que torna o VPL = 0. Esta taxa é importante para comparar se o investimento é mais rentável que outros investimentos, chamado de custo de oportunidade.

FinCal::irr(c(-1000, 100, 150, -200, 400, 200, 600))
#> [1] 0.048
FinCal::npv(0.048, c(-1000, 100, 150, -200, 400, 200, 600))
#> [1] 0.92

O valor do npv não se tornou zero devido ao calculo numérico do algoritmo.

Se TIR > custo de oportunidade -> Bom Investimento Caso contrário -> Permanecer com o investimento anterior

A TIR tem de ser maior do que a taxa de desconto (custo de capital)

11.5 Sistemas de amortização

O processo de quitação de um empréstimo consiste em efetuar pagamentos periódicos (prestações) de modo a liquidar o saldo devedor.

prestação = amortização + juros

Tipos de sistema de amortização:

  1. Sistema de amortização americano (SAA): Os empréstimos são quitados mediante o pagamento periódico de juros, deixando-se o principal para ser pago de uma única vez no final do último período

  2. Sistema de amortização francês (PRICE): O empréstimo é quitado mediante o pagamento de prestações fixas e constantes a cada período. Cada prestação inclui os juros mais uma parte de amortização (pagamento) do principal da dívida

Ex: Empréstimo de 10 mil reais a uma taxa de 5% ao ano

amort.table(Loan=10000,pmt=NA,n=10,i=.05,plot=T)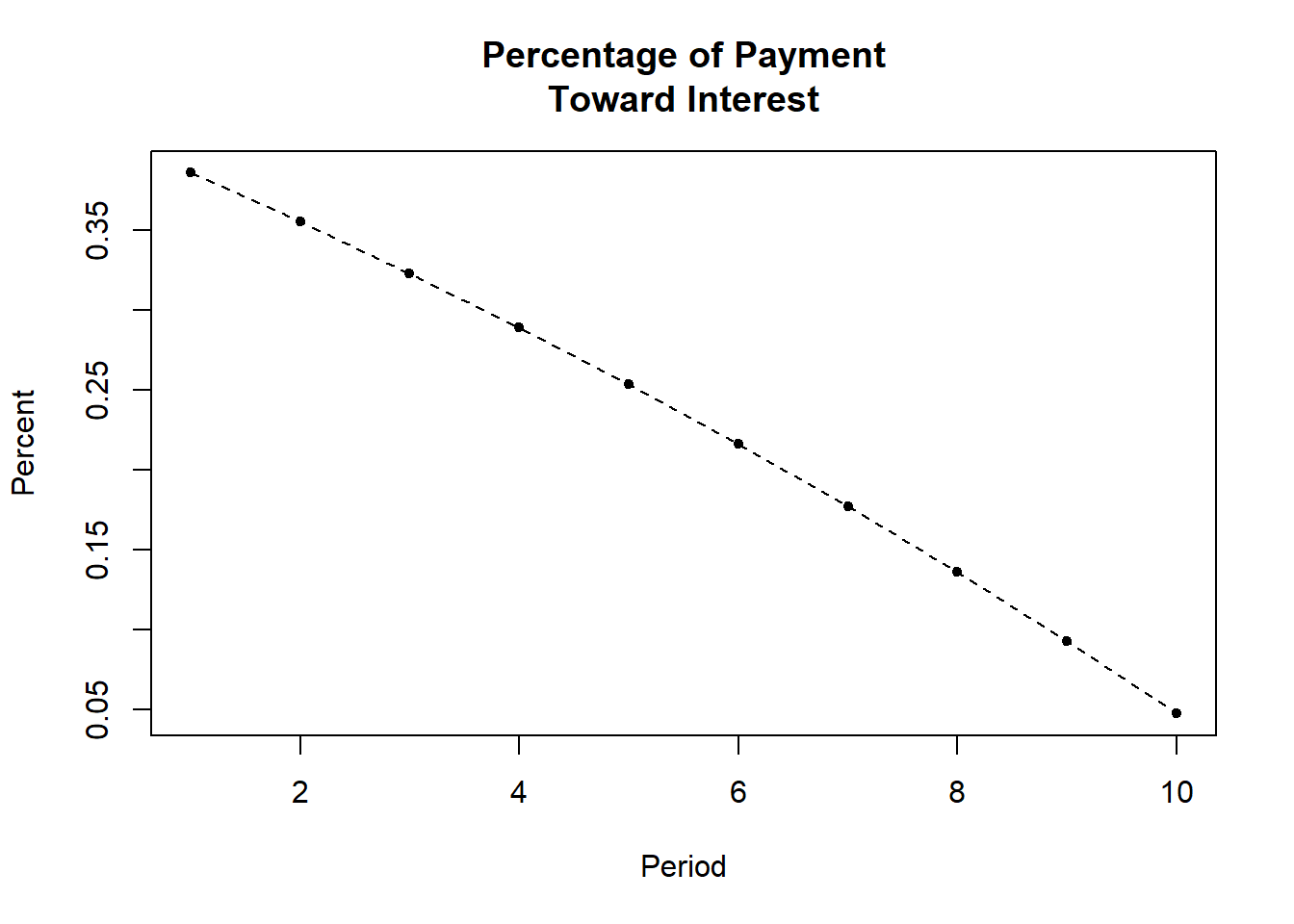
#> $Schedule
#>    Payment Interest Paid Principal Paid Balance
#> 1     1295           500            795    9205
#> 2     1295           460            835    8370
#> 3     1295           419            877    7494
#> 4     1295           375            920    6573
#> 5     1295           329            966    5607
#> 6     1295           280           1015    4592
#> 7     1295           230           1065    3527
#> 8     1295           176           1119    2408
#> 9     1295           120           1175    1233
#> 10    1295            62           1233       0
#> 
#> $Other
#>                 Details
#> Loan           10000.00
#> Total Paid     12950.46
#> Total Interest  2950.46
#> Eff Rate           0.05
  1. Sistema de amortização constante (SAC): O empréstimo é quitado com parcelas de amortização constantes ao longo do tempo. Como consequência, as prestações no SAC são decrescentes

Exemplo:

11.6 Outros cálculos no R 

#FinCalc
FinCal::fv.annuity(0.04, 10, 200,1)
#> [1] -2497
FinCal::r.perpetuity(200, -5000)
#> [1] 0.04
FinCal::npv(0.02, c(0,200,500,400,200,0,100))
#> [1] 1327
FinCal::irr(c(200,400,100,0,200,150))
#> [1] -1


#FinancialMath
FinancialMath::NPV(cf0 = 1000, cf = c(100,200,100,400, -500,200,600), times = c(1,3,3,4,3,5,6), i =  0.02, plot = T)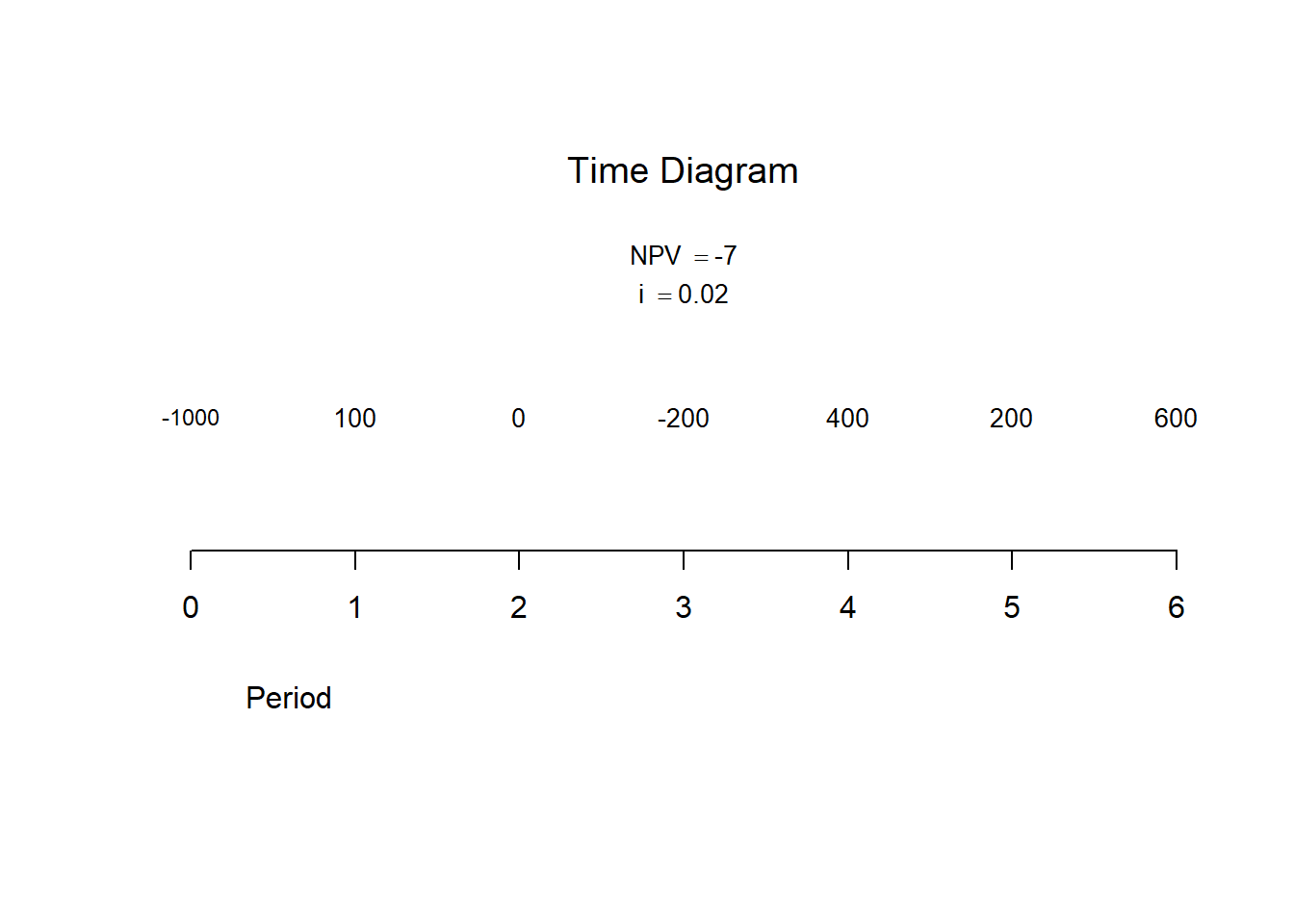
#> [1] -7
FinancialMath::TVM(1000, n = 50, i = 0.02, plot = T)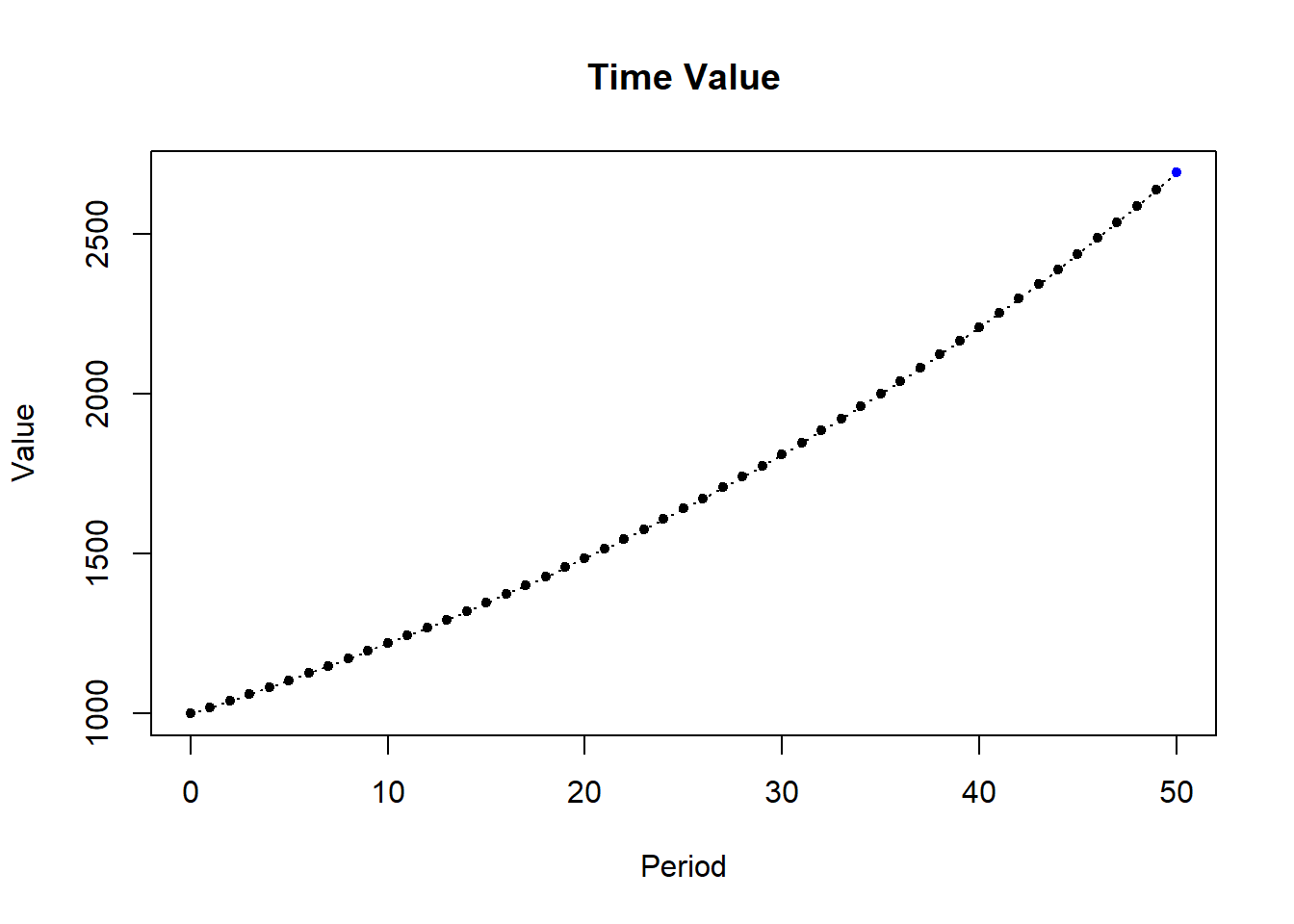
#>              TVM
#> PV       1000.00
#> FV       2691.59
#> Periods    50.00
#> Eff Rate    0.02

11.7 Bibliografia